Dimensionalizing Schooling
Creative CommUNITY Learning Encounters
by Vasiliki Tsigas-Fotinis, Ph.D.
Dimensionalizing Schooling
It’s time for Polyhedral Schooling:
The possibilities of Multidimensional Teaching and Learning
Have you ever visited a classroom in which everything in it seemed flat? The instruction, the relationships, the student’s work within the class and the homework, even the assessments seemed rather flat. The instruction was so linear and unidirectional, that any energy emitted just fizzed out. Conversely, have you ever visited a classroom in which everything in it seemed to continuously unfold dimension after dimension? The instruction seemed to go beyond the second dimension of a flat sheet of paper and surpass the realm of time, of space, of thought, of depth. Learning encountered in a variety of contexts and corresponding relationships. Learning is RELATIONAL. Relationships of the people in the class expanded beyond the confines of the classroom walls. In dimensional schools, the work students and teachers do, in and out of the classroom itself, seem to be purposeful, enjoyable, memorable, meaningful and fulfilling. Multiple dimensional learning experiences shape and sustain us in a way that the past and future energize and contextualize the present. Rich learning encounters are energized by a dynamic circular process of the teaching/learning dialectic relationship not bound by predefined roles or institutions.
It is time to explore the next dimension of learning -- to leave the land of illusion and enter a deeper reality. Plato in ancient times illustrated this concept for us in his allegory of the Cave, found in Book VII of The Republic. Today, Mathematicians and Physicists are discovering multiple dimensions and challenging us again to rethink what is illusion and what is reality. It is time for us in education to enter the next dimension in the way we are, think, and act as individuals, as schools, and as communities. Our systems of schooling, as well as the way we view and do learning need to go beyond the third dimension. Maxine Greene consistently reminds us to continue looking for endless possibilities. All because we do not yet see, may not mean it does not exist.
The chained prisoner, in Plato’s Cave, was released by another who guided him to experience reality beyond the cave. At first it was painful to see the fire which created the shadows on the cave wall, (his reality up to that moment). As he continued to ascend, with the help of his mentor, the sun too, initially caused him great pain, but that pain with the dimensions of contemplation, time and experience was transformed into great joy and appreciation for this new richer reality. The chained prisoners in Plato’s cave, whose only reality was the shadows they saw on the cave wall, brings to mind of the people in Edwin Abbot’s book “Flatland”, and their two-dimensional reality. Flatland is portrayed as a tessellation in which one of the geometric figures escapes their two-dimensional reality, enters the third-dimension, and begins a dialog with them. The difficulty of understanding each others’ perspective is wonderfully dialoged in Flatland. However in both books those who think beyond the experiential boundaries, who contemplate the uncontemplatable, and who think outside the shallowness of the two dimensional cave, begin to see the reality and beauty of other dimensions.
Genuine learning has numerous dimensions. Learning dimensions in terms of space, time, length, width, depth, height, magnitude, mass, in terms of energy, creativity, and a host of others are waiting to be explored. We in education tend to focus on many of the two-dimensional plains individually rather than on the relational character of the teaching-learning process existing in the third, fourth or nth dimension. In education we tend to separate and assign teaching and learning into separate entities, for particular roles, and to specific institutions. I would argue that teaching and learning are inseparable in every context in which they exist. Dimensional Learning examines the dialectic nature of teaching and learning and its relational character and context(s). Teaching and learning is an endless circular process much like how mathematics describes the higher levels of multiple dimensions. [See http://www.dimensions-math.org/Dim_E.htm] We need to identify the flat and shallow experiences in all that we interface with on a daily basis and continually work toward adding more depth and connections.
Ultimately we learn from the experiences we have; the contexts we live. Our five senses are like the dendrites of our experiential mind. In Mathematics, multiple dimensions are explained in terms of points, patterns, and their relationship to each other. Education should follow suit.
The roles of teacher and student in their relational dimension need to be developed and evaluated systematically, not separately. In describing teachers for the 21st century, Peter W. Cookson in his article What Would Socrates Say? (Cookson, 2009) said, “Teachers … would learn alongside their students, creatively adapting curriculum to their students’ needs.” This kind of teaching which is energized by its relationship to learning begins to take on a dimensional character. Socrates had a dimensional relationship with his students. The dimensions of depth, height, time, space, and breath existed within the context of their relationship. As one of the greatest teachers of all time Socrates was able to honestly say: “I know one thing, that I know nothing.” A teacher who ceases to learn, ceases to be capable of teaching. Likewise, systems of schooling that cease to learn and relate to the communal contexts of their clients cease to serve/educate.
Understanding Dimensional Relationships
Lev Vygotsky and others have said, ‘learning is social’. Therefore it follows that we need to teach, learn, and assess within that social dimensional context. All human interactions are multidimensional. It is not enough to just draw a line between point A and point B. The line without any kind of meaningful relationship cannot develop further into other dimensions. The word polyhedron comes from the Greek meaning many sides. There are many sides to every issue, not just pro’s and con’s. There are many sides to teaching and learning, and they work symmetrically together. We need to better understand the pattern these polyhedrons of the education process have, their multidimensional shape, to bring our schools through the shadows of our current reality… or is it an illusion?
In general, we tend to force all issues into two-dimensions, point A and point B. By doing so, we deny the reality of multifaceted dimensions that contextualize point A and point B, thus we tend to see the world as the people in Flatland did. We get so caught up with our rituals, and our own viewpoints—the shadows on the cave wall--that we defuse, deny and extinguish the reality of relationships and the organic dimensions they can bring us to. Some examples that I have observed include the discussions that separate and divide males and females, blacks and whites, and in education how we evaluate teaching and learning separately, even though in reality they exist in a multidimensional relationship. When I see a multiple choice test, I cringe at the prospect that we have flattened learning to a two-dimensional object which has a single direction. Learning and teaching are inseparable, continual and in reality go beyond the third dimension.
How many dimensions do each of us use in our teaching/learning? Hypothesis: The more dimensions used and the more related they are to each other, the deeper the learning, its retention and application. In mathematics this relation of a variety of points creates a unique pattern of a proportional number of cells, vertices, ends, angles, sides, triangles, circles or other shapes. How can we in education identify the points and corresponding relational patterns that create multidimensional schools in which multidimensional teaching and learning can exist and continue to grow?
A useful and practical way to test this hypothesis is for each of us to pose this question to all our educational networks of people, and they to their networks of educators as well, thus generating a Socratic style of endless questioning which brings us to infinite dimensions. Further exploration of Social Network Analysis and its application to educational systems may further our understanding to the social processes involved in dimensional educational systems.
“Learning never ends” takes on a deeper meaning when we share educational experiences with those around us. Just like when we learn by seeing and reading our context is merely two dimensions, but when we add learning by doing we enter the third dimension and sometimes even more dimensions. Multidimensionalizing schooling goes beyond the formal institution of education to what we do at home, work, in our web of relations, both virtual and physical, in social contexts such as the arts, sports, religions, cultures, languages and the myriad of social institutions we have created that we participate in.
Wisdom begins in wonder (Socrates). I wonder how considering the multiple dimensions of schooling as a process of education, of teaching and learning, may transform the lived experience of schooling for people around the world. We need to see the illusions and possible realities of the way we teach and learn. Our lived contexts cannot remain two-dimensional any longer. It is time to revisit Plato and enter the dimensions that no one has entered before.
References:
Abbott , Edwin A. (1884) Flatland: A Romance of Many Dimensions. Seely & Co., London, England.
[The movie: https://www.youtube.com/watch?v=RxcMa4lay5Q]
Cookson, Peter W. (2009) What Would Socrates Say? In ASCD’s Educational Leadership, September 2009, V.67, N.1., p.14.
Greene, Maxine (1980’s-90’s) her many insightful discussions offered at Teachers College. [See: https://maxinegreene.org]
Plato’s The Cave Based on an Allegory by Plato. Told by Orson Wells. Video Program #80805 SVE & Churchill Media, 6677 North Northwest Highway, Chicago, IL 60631 1-800-829-1900
[You-Tube: http://www.youtube.com/watch?v=d2afuTvUzBQ]
Jose Leys, Ètienne Ghys, Aurélien Alvarez (2008) Creative Commons http://www.dimensions-math.org/Dim_E.htm [For English explanation]; http://www.dimensions-math.org , dimensions@umpa.ens-lyon.fr An excellent video explanation of multiple dimensions!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~



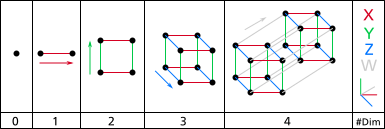
Comments
Post a Comment